For laminar boundary layers over a flat plate, the Blasius solution gives:
- the overall thickness (or height) of the boundary layer
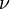 is the kinematic viscosity
is the kinematic viscosity is the distance downstream from the start of the boundary layer
is the distance downstream from the start of the boundary layer is the Reynolds Number
is the Reynolds Number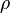 is the density
is the density is the freestream velocity
is the freestream velocity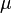 is the dynamic viscosit
is the dynamic viscosit
 ~10m/s,
~10m/s, 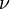 ~1.5e-6, x~2 m.
~1.5e-6, x~2 m.
with
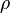 /
/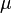 =
= 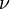
Re_x=
 * x /
* x / 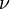 =1.33e7
=1.33e7 laminar=0.0027 m = 2.7 mm
laminar=0.0027 m = 2.7 mm turbulent=0.0287 m =28.7 mm
turbulent=0.0287 m =28.7 mmIn my mesh I will make 30 layers on the body with a total thickness of 30 mm. The thinnest layer will be 0.3 mm thick. With an expansionratio of 1.15 I will need 33 layers for 30 mm



No comments:
Post a Comment